KMP

分享到：

• 豆

1. 前言
2. 1.思想
3. 2.KMP模板题

前言

挺好用的一种字符串匹配算法。。。就是比较难懂。。。
KMP=Knuth-Morris-Pratt

1.思想

在不知道KMP算法的时候，大家应该都会从头到尾搜一遍，这样时间复杂度就是O(n*m)，n是字符串长度，m是子串的长度。
而KMP算法相对于暴搜的优化在于它往后跳的时候不是一个一个蹦的，有时候会一下跳好几个，这样就减少了搜索的次数。

下面讲解一下KMP的大致思想：
(假设被搜的字符串为a，去匹配的字符串叫b.以图片中的两行字符串为例，第一行为a，第二行为b.)

首先比较两个字符串的头：

发现并不匹配，于是往后跳一个字符，继续拿b的头与当前搜到的a的位置的字符比较：

一直到下图这种情况，发现能够匹配，那么就两个字符串同时往后扫：

当我们扫到b的D时，发现a的这个位置并不能匹配：

如果没有KMP，下一步就要让a再往后挪一个字符继续搜了：

---

但是！
我们有KMP啊，下面就是见证奇迹的时刻：

是不是很奇怪为什么要这样跳？
这里我们引入一个叫做“部分匹配值$^{[1]}$”的东东：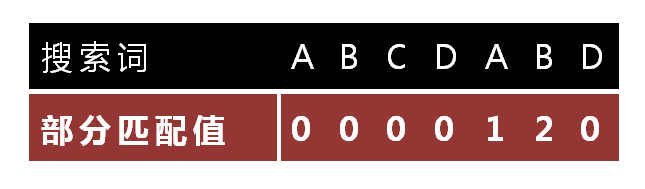

通常我们用一个next数组来储存它，往后跳的时候就把当前a上的指针加上当前已匹配的位数再减去失配时最后一个匹配的字符的部分匹配值

跳的位数 = 当前已匹配的位数 - 失配时最后一个匹配的字符的部分匹配值

6-2=4，所以就往后跳了4位：

然后就继续按照这个规则跳啊跳啊：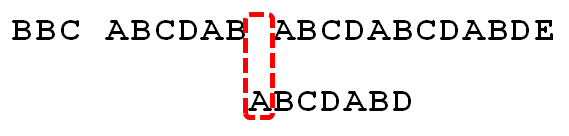

不匹配，继续跳

成功近在眼前

然后就完成了

---

[1]：“部分匹配值”表的制作过程：
（来自naivekun的博客，实在不想自己写了。。。）
1.首先，要了解两个概念：”前缀”和”后缀”。 “前缀”指除了最后一个字符以外，一个字符串的全部头部组合；”后缀”指除了第一个字符以外，一个字符串的全部尾部组合。

2.“部分匹配值”就是”前缀”和”后缀”的最长的共有元素的长度。以”ABCDABD”为例:

－　“A”的前缀和后缀都为空集，共有元素的长度为0；
－　“AB”的前缀为[A]，后缀为[B]，共有元素的长度为0；
－　“ABC”的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；
－　“ABCD”的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；
－　“ABCDA”的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为”A”，长度为1；
－　“ABCDAB”的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为”AB”，长度为2；
－　“ABCDABD”的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

3.“部分匹配”的实质是：有时候，字符串头部和尾部会有重复。比如，”ABCDAB”之中有两个”AB”，那么它的”部分匹配值”就是2（”AB”的长度）。搜索词移动的时候，第一个”AB”向后移动4位（字符串长度-部分匹配值），就可以来到第二个”AB”的位置。

2.KMP模板题

【题目链接】
洛谷【3375】
【题目描述】
如题，给出两个字符串s1和s2，其中s2为s1的子串，求出s2在s1中所有出现的位置。
为了减少骗分的情况，接下来还要输出子串的前缀数组next。如果你不知道这是什么意思也不要问，去百度搜[kmp算法]学习一下就知道了。
【输入格式】
第一行为一个字符串，即为s1（仅包含大写字母）
第二行为一个字符串，即为s2（仅包含大写字母）
【输出格式】
若干行，每行包含一个整数，表示s2在s1中出现的位置
接下来1行，包括length(s2)个整数，表示前缀数组next[i]的值。
【输入样例】

ABABABC
ABA

【输出样例】

1
3
0 0 1

【程序】

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#define M 5000000

using namespace std;

int la,lb;
char a[M],b[M];
int next[M];

inline void getnext()
{
    next[0]=-1;
    for(int i=2,j=0;i<=lb;++i,++j)
    {
        while(j!=-1&&b[i]!=b[j+1]) j=next[j];
        next[i]=j+1;
    }
    
}

inline void kmp()
{
    for(int i=1,j=0;i<=la;++i,++j)
    {
        while(j!=-1&&a[i]!=b[j+1]) j=next[j];
        if(j==lb-1) printf("%d\n",i-j);
    }
}

int main()
{
    scanf("%s",a+1);
    scanf("%s",b+1);
    la=strlen(a+1);
    lb=strlen(b+1);
    getnext();
    kmp();
    for(int i=1;i<=lb;++i)
        printf("%d ",next[i]);
    return 0;
}

上一篇

下一篇